Инженерные задачи исследования аддитивного производства обладают рядом особенностей, к числу которых можно отнести геометрию расчётной области, сложные физико-­химические процессы, а также ограничения, накладываемые на параметры производственной системы. При расчёте технологических параметров процесса электронно-­лучевого сплавления (EBM) необходимо выполнить моделирование взаимодействия электронного пучка с подложкой, сплавления слоя порошка с подложкой, растекания материала на базе системы, состоящей из уравнений изменения энергии, изменения количества движения (уравнения Навье —Стокса) и уравнения неразрывности.

Моделирование процесса формирования слоя

В основе моделирования процесса формирования слоя лежит решение нелинейных дифференциальных уравнений изменения энергии, изменения количества движения (уравнения Навье — Стокса) и уравнения неразрывности. При воздействии на материал электронным пучком происходят фазовые переходы в условиях сильной неравновесности. Учёт неравновесного характера протекающих процессов основывается на рассмотрении фазового состояния ячейки подложки в зависимости от энтальпии и времени ожидания появления зародыша новой фазы. Другой подход основан на решении задачи Стефана с привлечением нелинейной зависимости скорости движения границы раздела фаз от температуры. При моделировании необходимо учитывать зависимость теплофизических свой­ств материала порошка (удельной теплоемкости, теплопроводности и плотности) от температуры.

Особенностью процесса формирования слоя электронным пучком является движение жидкой проводящей поверхности под действием электрического и магнитного полей. Чтобы учесть влияние жидкого проводящего слоя в электромагнитном поле вследствие воздействия электронного пучка, в правую часть уравнения теплопроводности добавим дополнительное слагаемое:

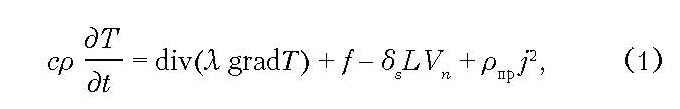
где ρпр — проводимость жидкого металла, j — плотность тока внутри жидкости.

Дифференциальное уравнение движения жидкости в области расплавленного слоя имеет следующий вид:

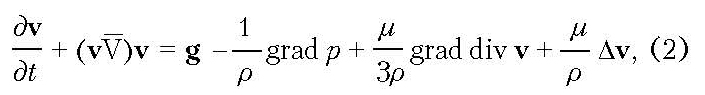
где g = (0,0, g) — ускорение свободного падения; ρ — плотность; p — давление; μ — коэффициент динамической вязкости; v = (vx, vy, vz) — вектор эффективной скорости расплава, рассчитываемый через истинную скорость жидкой фазы.

Плавление материала порошка осуществляется электронным пучком. В центре пятна на поверхности температура максимальная, уменьшается к краю пятна, что создаёт температурный градиент на свободной поверхности. При плавлении возникает движение жидкости. Это приводит к сложным термокапиллярным течениям вследствие зависимости поверхностного натяжения от температуры. Эффекты, связанные с движением жидкости вблизи поверхности раздела и вызванные зависимостью коэффициента поверхностного натяжения от температуры или концентрации примесей, называется эффектом Марангони. Действующая на поверхность ванны расплава сила Марангони приводит к перемешиванию расплава от центра к краям слоя.

Зависимость коэффициента поверхностного натяжения (σ) от температуры можно определить через следующую формулу:

             dσ/dT = –B(ρ/μM)^2/3,

где T — температура; μM — молекулярная масса; 

B — постоянная, равная 2,1 г.см²/(с.°С).

Зависимость коэффициента динамической вязкости от температуры может быть приближенно представлена уравнением Френкеля — Андраде:

μ = A₁ exp (E_η /RT),

где E_η — свободная энергия активации; R — универсальная газовая постоянная; T — температура по абсолютной шкале; A₁ — константа, зависящая от химической природы вещества. Константу A1 можно рассчитать по уравнению Эйнштейна:

A₁ = Nh/V, где N — число Авогадро, h — постоянная Планка, V — мольный объем. Порядок величины A₁ составляет 10^–4–10^–5 Па·с.

Так как объектом плавления является порошок шаровидной формы, то поверхность раздела двух сред искривлена. Следовательно, давления в обеих средах различны. Коэффициент поверхностного натяжения жидкости, который равен работе, необходимой для увеличения поверхности жидкости на единицу площади при постоянной температуре, зависит от свой­ств жидкости и среды, с которой граничит жидкость.

Поверхность жидкого металла стремится принять свою равновесную форму под влиянием силы тяжести и сил поверхностного натяжения. Следует отметить, что влияние капиллярности на гравитационные волны существенно при малых длинах волн. Тогда дифференциальное уравнение движения жидкости имеет следующий вид:

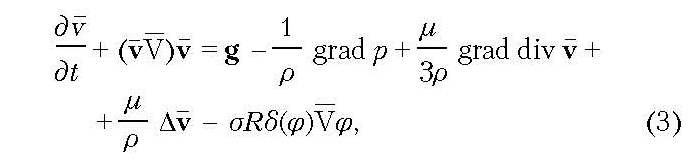
где R — искривление линии раздела двух фаз; φ — расстояние от текущей линии раздела двух фаз до нулевого интерфейса; δ(φ) — волновая функция от φ.

Последняя составляющая уравнения (3) позволяет учесть волновой характер процессов на свободной поверхности, разделяющей поверхности двух фаз: жидкости и вакуумного пространства.

Уравнения теплопроводности имеют вид:

— твердая фаза, (x, y, z, t)Q^–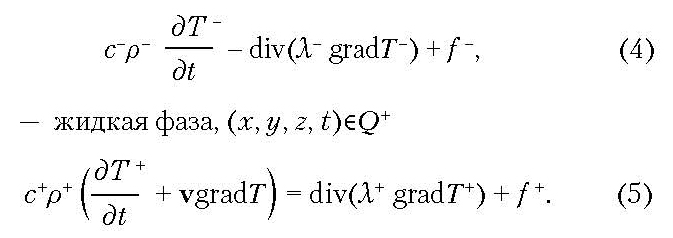

Здесь c– и c+ — теплоёмкость материала соответственно в твёрдом и жидком состояниях; λ– и λ+ — коэффициент теплопроводности материала в твёрдом и жидком состояниях; ρ– и ρ+ — плотность материала в твёрдом и жидком состояниях; T– и T+ – температура материала в твёрдом и жидком состояниях; f – и f + — плотности тепловых источников в твёрдом и жидком состояниях.

В жидкой фазе учитывается также конвективный перенос. В уравнении теплопроводности функция f представляет собой плотность распределённых массовых источников тепла, находящихся внутри расчётной области.

На границе фазового перехода S (граница контакта двух сред) выполняется условие непрерывности температуры

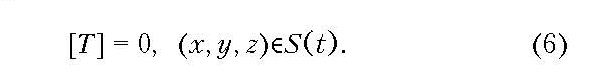
Квадратные скобки используются для обозначения скачка температуры.

Фазовый переход сопровождается выделением/поглощением определённого количества тепла, поэтому тепловой поток на границе фазового перехода разрывной:

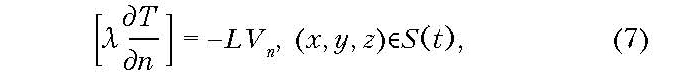
где L — энтальпия фазового перехода, Vn — скорость движения границы фазового перехода по нормали.

При постоянной температуре фазового перехода граница в каждый момент времени определяется следующим образом:

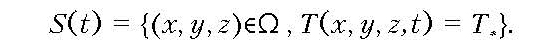
На границе фазового перехода выполняются граничные условия первого рода

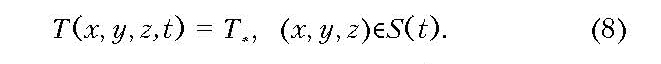
Условия (6)–(8) представляют собой условия Стефана, а соответствующая задача для уравнений (4) и (5) называется задачей Стефана. Рассматриваемая задача характеризуется тем, что исследуются процессы в обеих фазах, поэтому в данном случае говорят о двухфазной задаче Стефана. В предельной ситуации тепловое поле в одной из фаз известно (температура равняется температуре фазового перехода), поэтому рассматривается тепловое поле только одной из фаз  — однофазная задача Стефана, в которой граница фазового перехода S не внутренняя, а внешняя.

Рассмотрим переход от уравнений (4) и (5) с условиями (6)–(8) к одному уравнению теплопроводности. Уравнения (4) и (5) допускают запись в виде одного уравнения:

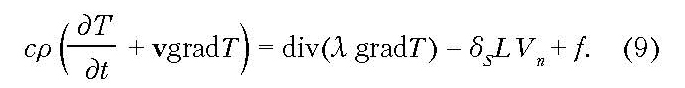
Здесь c — теплоёмкость материала, λ — коэффициент теплопроводности материала, ρ — плотность материала, T — температура, f — плотность теплового источника, δS — поверхностная δ-функция, Vn — скорость движения границы фазового перехода по нормали, L — энтальпия фазового перехода.

Уравнение неразрывности имеет следующий вид:

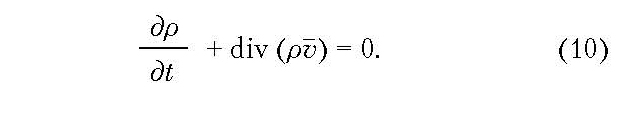
Таким образом, тепло- и массоперенос описывается уравнениями (3), (9), (10) для трёх неизвестных: температуры T, вектора скорости движения жидкого металла v, давления p. Дополним систему уравнений (3), (9), (10) необходимыми граничными и начальными условиями.

На рис. 1 представлены основные области модели: О₁ — верхняя область расплавленного металла, О₂ — твёрдая поверхность формируемого изделия, О₃ — область подложки, О₄ — боковые поверхности расплавленного слоя металла. В области О₁ рассматривается неизотермическое течение сжимаемой ньютоновской жидкости, объёмная тепловая нагрузка вследствие действия электронного пучка, радиационное тепловое излучение на внешнюю стенку вакуумной камеры, в О₂ — процессы остановки движения жидкого металла к твёрдой поверхности; в О₃ — тепловая масса, моделирующая подложку; в О₄ — процессы размерной обработки по боковой поверхности синтезируемого изделия.

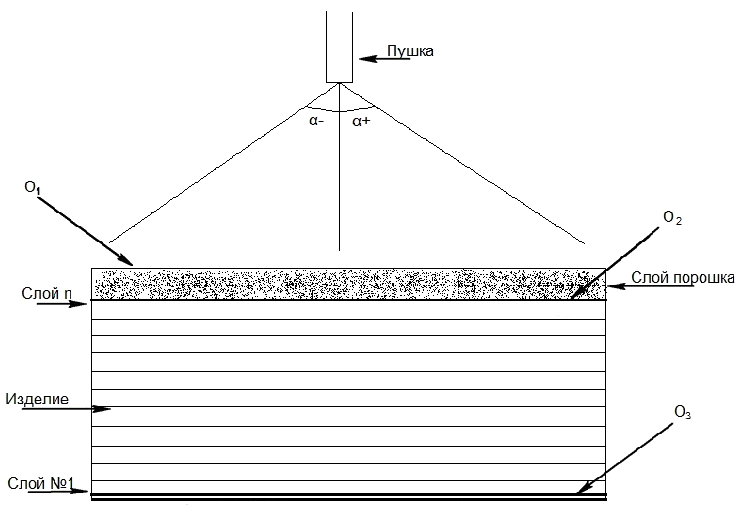
Рис. 1. Области модели процесса

Граничные условия модели:

1. Скорость движения жидкого металла v области О₂ равна нулю (условие полного сплавления слоя порошка с твёрдой поверхностью подложки).

2. При расчёте теплообмена излучением необходимо учитывать потоки, попадающие на экраны, установленные в вакуумной камере установки, в областях О₁, О₃, О₄. С поверхности подложки тепло теряется излучением по закону Стефана — Больцмана, т. е. имеем краевую задачу с нелинейным граничным условием:

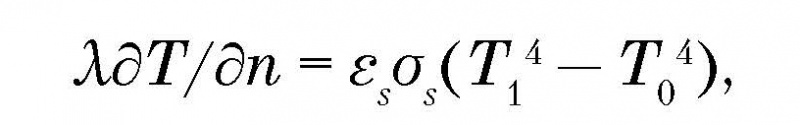
где T0 — температура на тепловом экране, T1 — температура на поверхности подложки, σs — постоянная Стефана — Больцмана (1,38044 . 10–23 Дж/град), εs — степень черноты, ∂/∂n — нормаль к границе поверхности.

3. В области О1 задают граничные условия второго рода (условия Неймана), соответствующие заданию на границе распределённого теплового потока. Для уравнения теплопроводности в изотропной среде оно записывается в виде:

 λ∂T/∂n = qt , где qt — тепловой поток.

4. Уравнение свободной (верхней) поверхности

φ(x, y, z,t) жидкого металла имеет следующий вид:

Начальные условия: свободная поверхность является плоской и известно начальное распределение скорости на ней (v₁ = v₂ = v₃ = 0), температура в точках свободной поверхности равна 20°С.

Перечисленные задачи нелинейные, требуют применения численных методов. Нелинейность задач обусловлена зависимостью не только теплофизических параметров материала от температуры, но и источника тепла от времени (периодическое воздействие пучка на подложку), т. е. задачи являются нестационарными. Для их решения используются программные пакеты ANSYS APDL и ANSYS Workbench.

Расчёт формирования слоя с учётом теплоты фазового перехода

Решение задачи моделирования формирования слоя изделия позволяет определить важнейшие параметры процесса EBM (скорость нагрева и охлаждения слоя порошка, время плавления и кристаллизации порошка, скорость перемещения твёрдо-­жидкой границы и др.), которые определяют свой­ства и структуру изделия.

В качестве инструмента моделирования выбран программный комплекс ANSYS Workbench, пространственный режим 3D, режим расчёта динамический, тепловой режим неадиабатный.

При моделировании процесса формирования слоя задаются:

1. Теплофизические параметры: температура солидус Tsol, температура ликвидус Tliq, коэффициент теплопроводности λ, удельная теплоёмкость cυ, плотность материала ρ, приведённая степень черноты εпр, коэффициент поверхностного натяжения σ, динамическая вязкость расплава μ.

2. Параметры электронного пучка: ток I, ускоряющее напряжение U, диаметр пятна на мишени do, скорость сканирования Vs, шаг смещения при сканировании s.

Исходные данные математической модели: материал порошка — титан, диаметр порошка — 50 · 10^–6 м, высота подложки — 0,1 м, температурный интервал между температурами солидус и ликвидус — 100°С, температура солидус Tsol = 1570°C, температура ликвидус Tliq = 1670°C. Подложка моделируется тепловой массой со значением теплового захвата  3,4069 · 10^–2 Дж/°С.

К основным этапам нестационарного теплового анализа относятся: проектирование модели, задание граничных условий и тепловых нагрузок, решение задачи на основе уравнения теплопроводности и анализ результатов.

Процедура создания модели включает задание типа элементов, свой­ств материала и геометрии модели. Далее выполняется наложение сетки на модель (создание конечно-­элементной модели) и задаются граничные и начальные условия. Так как в начальный момент времени температура модели совпадает с температурой окружающей среды, то в качестве начальной температуры для всех узлов модели принимают температуру окружающей среды.

В исследованиях приводится нелинейная зависимость теплопроводности титана до температуры 1300°, до температуры 1660°С. Для получения значений коэффициента теплопроводности при более высоких температурах, необходимых при моделировании процесса охлаждения частиц с учётом фазового перехода, воспользуемся полиномом 4 степени, Вт/(м К):

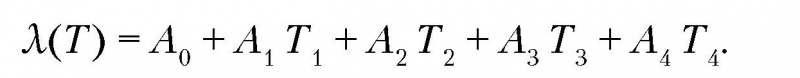
Для нахождения коэффициентов Ai используем метод наименьших квадратов. В результате решения системы уравнений с 5 неизвестными имеем:

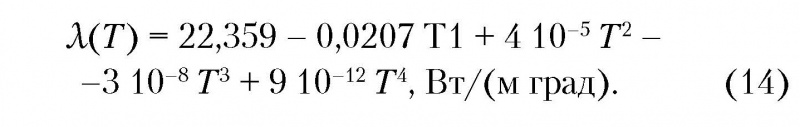
Функциональная зависимость плотности титана от температуры имеет следующий вид:

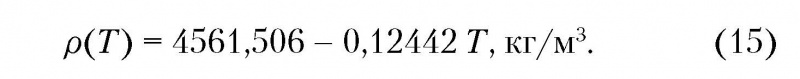
Температура в формулах (14) и (15) измеряется в градусах Цельсия. Значительные изменения теплопроводности и плотности ρ(T) показывают, что система дифференциальных уравнений тепло- и массопереноса, описывающая формирование слоя порошка, существенно нелинейная.

Нелинейная зависимость теплопроводности, плотности и теплоёмкости титана от температуры видна на графиках. Для температур до 1100°С характерен участок с малыми значениями коэффициента теплопроводности, что соответствует высокой скорости нагрева. При более высоких температурах наступает резкое нелинейное увеличение коэффициента теплопроводности.

Значительные изменения теплопроводности λ(T)и плотности ρ(T) показывают, что система, описывающая процесс EBM, существенно нелинейная.

Для расчёта динамической вязкости титана применяется следующая формула:

— μ — коэффициент динамической вязкости;

— mA — атомная масса;

— kb — постоянная Больцмана;

— T — температура;

— σ(T) — коэффициент поверхностного натяжения расплава.

Коэффициент поверхностного натяжения частицы, равный работе, необходимой для увеличения поверхности жидкости на единицу площади при постоянной температуре, зависит от свой­ств расплава и охлаждаемой среды. При моделировании необходимо учитывать зависимость коэффициента поверхностного натяжения от температуры.

Основные физические постоянные для титана имеют следующие значения:

— mA = 47,9 1,6605 10^–27 кг = 79,54 10^–27 кг;

— kb = 1,380662 10^–23 Дж/К;

— σ = 1,56 кг с^‒2.

Тогда рассчитанный по формуле (16) коэффициент динамической вязкости титана

              μ = 2,843 10^–3 кг м^‒1 с^‒1.

Нагрев каждой элементарной ячейки происходит за время, равное времени перемещения электронного пучка над этой ячейкой. В нашей задаче нагрев эквивалентен приложению тепловой нагрузки треугольной формы:

                         t = 2d₀/V_s.

Граничные и начальные условия ММ представлены графически (рис. 2):

— области A и B (верхняя и нижняя поверхности изделия) — радиационное тепловое излучение на экран вакуумной камеры;

— область C — переменная начальная температура по глубине изделия;

— область D, E — начальная температура предварительного нагрева (1000°С);

— область F — начальная температура подложки;

— область G — тепловой поток, приложенный к элементарному объёму;

— область H — точечная тепловая масса, моделирующая подложку.

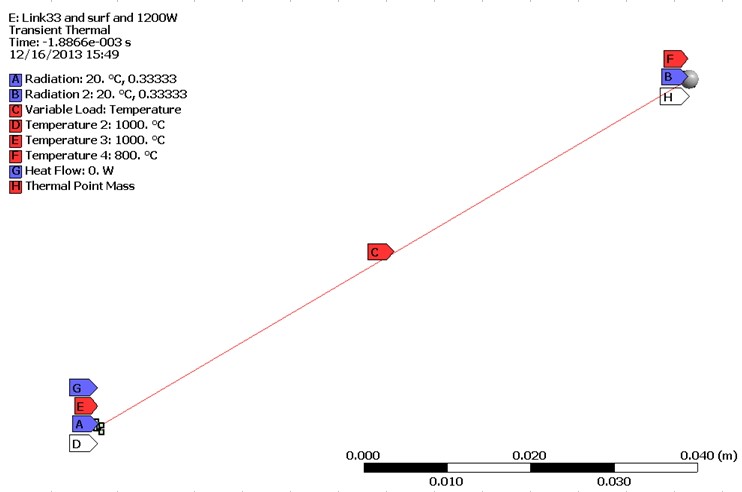
Рис. 2. Граничные и начальные условия модели 

Охлаждение на границах изделия — окружающая среда задаётся через лучистый теплообмен (передача тепла посредством электромагнитных волн) поверхности подложки и стенок тепловых экранов. При расчёте теплообмена излучением необходимо учитывать потоки тепла в областях, попадающих на экраны, установленные в вакуумной камере установки. С поверхности подложки тепло теряется излучением по закону Стефана — Больцмана.

В верхней области формируемого изделия задаём граничные условия второго рода (условия Неймана), соответствующие заданию на границе распределённого теплового потока. Уравнение теплопроводности в изотропной среде записывается в следующем виде:

                    λ ∂T/∂n = q(t).

Начальные условия:

1) приведённая степень черноты излучательных потоков εпр = 0,334;

2) температура окружающей среды и тепловых экранов 20°С;

3) распределение температуры в зависимости от координаты z: при 0 ≤  z  ≤  0,1 м T(z) = 800 + (z/0,1)0,3 200; при 0,1 <  z < 0,10005 м T(z) = 1000.

Типы конечных элементов, используемых в модели:

— LINK 33 — линейный элемент, моделирующий теплопроводность;

— SURF152 — поверхностный элемент (нагрузка в виде излучения).

Рассмотрим результаты моделирования процесса при диаметре пучка d0 = 0,6 мм. На элементарный объём промоделировано одно воздействие электронного пучка. Изменение температуры на поверхности порошка T_UP, на границе слоёв T_GR при воздействии электронного пучка мощностью 900 Вт представлено на графиках, где отражено влияние скрытой теплоты плавления на процессы нагрева и охлаждения (рис. 3).

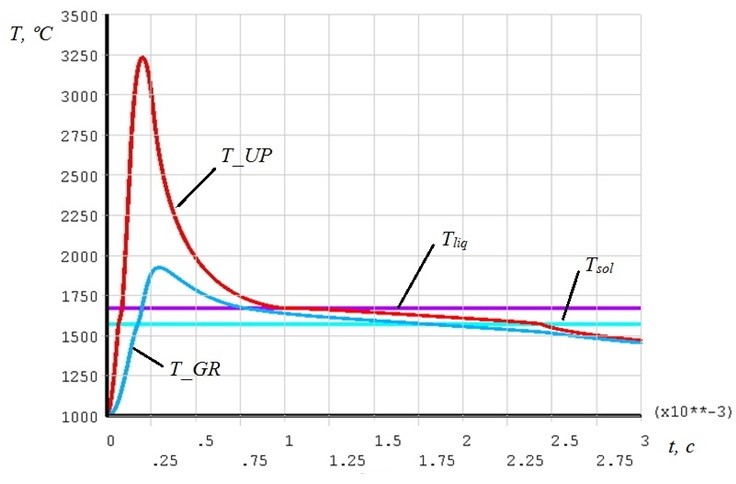
Рис. 3. Изменение температуры на границах слоя порошка в результате первого воздействия пучка мощностью 900 Вт (диаметр пучка 0,6 мм)

При исследовании перемещения твёрдо-­жидкой границы задаётся малый интегральный шаг по времени (рис. 4).

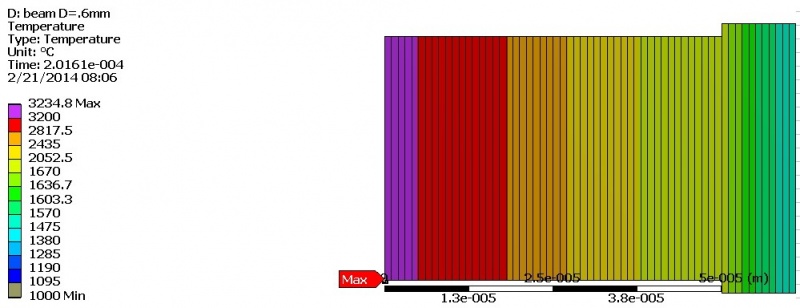
Рис. 4. Глубина фазового перехода после первого воздействия пучка диаметром 0,6 мм

В зависимости от теплофизических характеристик материала порошка и режима обработки поверхности порошка электронным пучком граница раздела твёрдо-­жидкой фазы перемещается с различной скоростью.

Модель позволяет рассчитать скорость перемещения твёрдо-­жидкой границы, глубину проплавления, скорости нагрева и охлаждения материала при воздействии электронного пучка различной мощности. Таким образом, математическая модель позволяет рассчитать параметры процесса EBM. ■

Авторы:  В.В. Константинов, к.т.н., генеральный директор публичного акционерного общества «Электромеханика»

Ю.А. Соколов, д.т.н.,  заместитель коммерческого директора публичного акционерного общества «Электромеханика»

Источник журнал "Аддитивные технологии" № 2-2021