14.00

Normal
0

false
false
false

RU
X-NONE
X-NONE

  Введение  

В математической теории горения [1] дана обобщенная математическая постановка задачи определения скорости горения, состоящая из уравнения переноса тепла с учётом скорости тепловыделения от химической реакции и выгорания реагентов. Система уравнений, описывающая распространение пламени в горючей среде, записывается в безразмерных переменных и параметрах [1]. В зависимости от определяющих параметров задачи, граничных условий, условий теплообмена могут возникать различные режимы горения: устойчивые, автоколебательные, неустойчивые; наблюдается также срыв распространения пламени, который происходит при сильном теплоотводе из зоны химической реакции [2-4]. При распространении пламени в безгазовых конденсированных системах важную роль играет гетерогенная структура вещества. В работах [3, 4] для описания гетерогенной структуры СВС составов была предложена модель реакционной ячейки. Задачи [3, 4] решены в стационарной постановке. В работе [5] приведено численное моделирование процесса горения конического образца при теплоотводе в квазиодномерной постановке задачи.

Целью настоящей работы является проведение численного исследования нестационарного безгазового горения в коническом образце при наличии теплоотвода на внешних границах в двухмерной осесимметричной постановке. Моделирование горения конического образца проводится с учетом гетерогенности его структуры с использованием модели сферических реакционных ячеек.

Постановка задачи

Реакционная ячейка представляется в форме шарика, состоящего из вещества A, окруженного веществом B (Рис. 1).

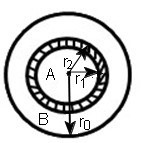
Рис.1 Сферическая реакционная ячейка

Вещества находятся в заданном стехиометрическом соотношении. На границе контакта веществ А и В будет образовываться продукт реакции АВ. Для моделирования распространения волны безгазового горения в однородной смеси порошков реакционные ячейки располагаются непрерывным образом по длине образца. При распространении волны горения по образцу по мере прогрева реакционных ячеек в них активируется диффузия, происходит реакция и нарастание слоя продуктов реакции в каждой реакционной ячейке. Размеры реакционных ячеек предполагаются одинаковыми, плотности веществ A, B и продукта AB также одинаковы. Скорость химического реагирования в каждой точке по длине образца СВС определяется из решения задачи диффузии и химического реагирования в реакционных ячейках, учитывается диффузия через образующийся слой продукта и зависимость коэффициента диффузии от температуры. Предполагается, что пространственное распределение температуры в реакционной ячейке отсутствует. Обоснование такого предположения проведено в [4] на основе сравнения характерных масштабов диффузии и теплопроводности. Также предполагается, что коэффициент диффузии зависит от температуры по экспоненциальному закону.

Для анализа структуры фронта горения СВС систем проводятся экспериментальные исследования, заключающиеся в том, что смесь порошков, запрессованную в коническую проточку в медной массивной подложке, зажигают. При зажигании СВС состава фронт горения распространяется по образцу, после чего затормаживается за счет теплоотдачи в массивную медную подложку. После остывания образца его разрезают для анализа структуры волны горения. Математическое моделирование данного процесса необходимо, так как может показать степень изменения глубины превращения исходных компонентов после «затормаживания» фронта горения в процессе его остывания.

В данной работе приведено решение задачи безгазового горения конического образца с использованием модели сферической реакционной ячейки [6]. Математическая постановка в двухмерном осесимметричном варианте в безразмерной форме имеет вид:

.      (1)

Начальные и граничные условия:

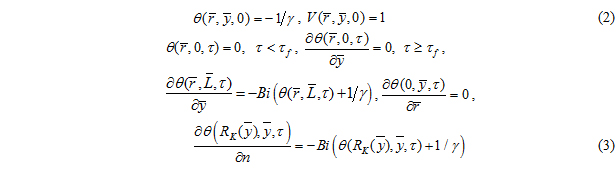
Величина тепловыделения от химической реакции в уравнении (1) определяется из решения задач диффузии и реагирования на микроуровне в реакционной ячейке:

,      (4)

(5)

В уравнении (1):

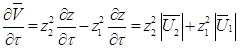        (6)

Значения  и  определяются из соотношений:

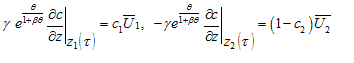(7)

Система уравнений записана в традиционных для теории горения безразмерных переменных и параметрах [1]. В качестве масштабов выбрано: масштаб времени ; масштаб координаты на макроуровне ; масштаб температуры ; масштаб координаты для реакционной ячейки . Обозначения: с – удельная теплоемкость; p – плотность; T  – температура; t – время; лямда – коэффициент теплопроводности; r, y – радиальная и осевая координаты цилиндрической системы координат; b – концентрация реагента; R_k (y) – внешний радиус конической части образца; L – высота конической части образца; E – энергия активации; Q – тепловой эффект реакции; k₀ – предэкспоненциальный множитель; T_a – адиабатическая температура горения; R – универсальная газовая постоянная; t_f – момент времени, когда граничное условие первого рода переключается на граничное условие, соответствующее адиабатической границе; альфа – коэффициент теплоотдачи; n – направление нормали к боковой поверхности конической части образца.

Безразмерные переменные: координата ; время: ; температура ; объём , где r - радиальная координата гетерогенной структуры, r_* = r₀ - масштаб координаты для реакционной ячейки r_* = r₀ - ее радиус. Также в задаче введены безразмерные параметры определяемые следующим образом:

.

Для решения системы уравнений (1) – (3) проводилось преобразование координат, связанное с формой образца. Полученное в преобразованных координатах уравнение решалось по явной схеме. Для определения величины источников уравнения (1), определяемых в виде (4), в каждой точке пространства (в каждой точке разностной сетки) решалась задача (4) – (7).

Численные расчёты задачи (1) – (7) проводились при , параметр R_K (0) принимал значения .

Анализ результатов

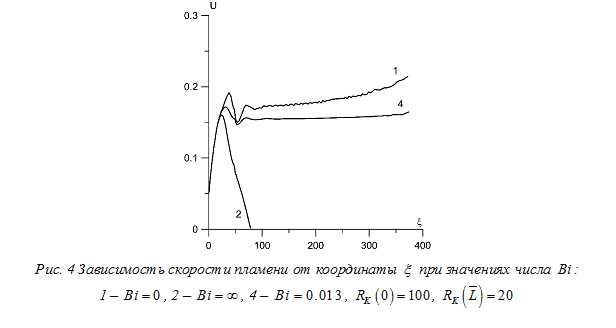
На рисунке 2 показаны зависимости скорости горения СВС состава от координаты  при различных значениях числа Bi при R_K (0) = 200. На графике показано три режима распространения фронта горения: 1) увеличение скорости фронта горения с пройденным расстоянием вдоль оси конуса (кривая 1). Наблюдается при значении Bi = 0; 2) срыв (погасание) горения (кривая 2). Наблюдается при значениях . Из графика видно, что при  происходит срыв горения на расстоянии  от правой границы (меньшего основания) конуса; 3) срыва горения не наблюдается (кривая 3). Данная кривая была получена в результате проведения вычислительных экспериментов по определению значения числа Bi, при котором срыва горения в коническом образце не происходит, сгорание конического образца происходит с почти стационарной скоростью. Кривая 3 соответствует числу Bi = 0.033.

Для случая, когда происходит срыв горения, поля температуры и концентрации представлены на рисунке 3. Подобные вычислительные эксперименты были проведены и для R_K (0) = 150, R_K (0) = 100. Результаты расчетов при R_K (0) = 100 представлены на рисунках 4, 5.

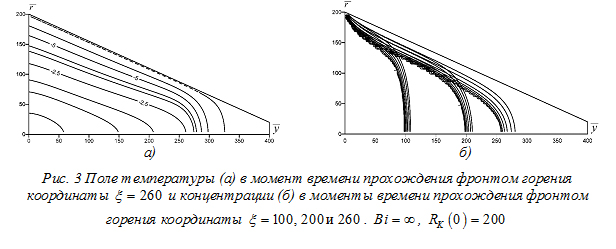
Для случая, когда происходит полное сгорание конуса, поля температуры и концентрации представлены на рисунке 5.

Из вычислительных экспериментов следует, что критическое значение параметра Bi, при котором срыва горения конического образца не происходит, принимает разные значения для различных R_K (0). Для R_K (0) = 200 было определено Bi = 0.035, для R_K (0) = 150  – Bi = 0.025, для R_K (0) = 100 – Bi = 0.015. Таким образом, определены посредством вычислительного эксперимента критические величины теплоотвода, приводящие к срыву горения.

Заключение

Таким образом, проведено численное исследование распространения волны горения в коническом образце СВС состава при наличии теплоотвода на внешних границах в двухмерной осесимметричной постановке. Определены посредством вычислительного эксперимента критические величины теплоотвода, приводящие к срыву горения. Определены величины недогоревшего слоя в зависимости от интенсивности теплоотдачи и геометрических величин конического образца СВС состава. Проведен сравнительный анализ результатов расчетов скорости для двух моделей безгазового горения с учетом и без учета гетерогенности структуры СВС состава конического образца. Анализ показал, что зависимости скорости распространения волны безгазового горения качественно совпадают. 

Исследование выполнено за счет гранта Российского научного фонда (проект №17-79-20011).

Автор:

14.00

Normal
0

false
false
false

RU
X-NONE
X-NONE

Крайнов А.Ю. ^1,a, Шульц Д.С. ^2,b

¹ Национальный исследовательский Томский государственный университет
Россия, г.Томск, пр. Ленина, 36, 634050

² Томский государственный университет систем управления и радиоэлектроники
Россия, г.Томск, пр. Ленина, 40, 634050

E-mail: ^aakrainov@ftf.tsu.ru, ^b d_schulz@mail.ru

Список литературы

1. Зельдович Я.Б., Баренблатт Г.И., Либрович В.Б. и Махвиладзе Г.М. Математическая теория горения и взрыва / М: Наука. 1980. – 478 с..

2. Мержанов А.Г., Мукасьян А.С. Твердопламенное горение / М.: ТОРУС ПРЕСС. 2007. – 336 с.

3. Алдушин А.П., Мержанов А.Г., Хайкин Б.И. О некоторых особенностях горения конденсированных систем с тугоплавкими продуктами реакции / Докл. АН СССР. 1972. – Т. 204, № 5. – С. 1139-1142.

4. Хайкин Б.И. К теории процесса горения в гетерогенных конденсированных средах, Процессы горения в химической технологии и металлургии / Черноголовка: Изд-во ОИХФ АН СССР. 1975. – С. 227-244.

5. Stepanov B.V., Rogachev A.S. Quenching of solid-phase combustion front of a symmetric sample by supercritical heat loss / International Journal of Self-Propagating High-Temperature Synthesis. 1992. – Vol. 1, Iss. 3. – P. 409-416.

6. Крайнов А.Ю., Шульц Д.С. Математическое моделирование СВС процесса в гетерогенных реагирующих порошковых смесях / Компьютерные исследования и моделирование. 2011. – Т. 3, № 2. – С. 147-153.