Введение

Селективное лазерное плавление (СЛП) [1] металлических порошков реализуемо с помощью непрерывного или импульсного лазера. В большинстве промышленных машин для 3D печати применяются непрерывные лазеры, так как при таком методе плавления достигаются квазистационарные тепловые условия в зоне расплава. Это способствует достижению стационарных условий кристаллизации и теплоотвода, что, в конечном счете, улучшает механические свойства изготавливаемых изделий и обеспечивает приемлемую скорость послойного изготовления компактов.

При решении ряда практических задач методом СЛП удобнее использовать  импульсные лазеры (ИЛ). Например, импульсная лазерная оснастка необходима для изготовления изделий с высоким коэффициентом отражения. В этом случае традиционная конфигурация с непрерывным лазером не обеспечивает температур, достаточно высоких для плавления таких порошков. Другим применением является изготовление градиентных функциональных покрытий, образованных в виде композиционных неравновесных фаз и структур. Это привело к созданию разновидности СЛП – метода высокоскоростного лазерного плавления (ВЛП) [2]. Отметим, что импульсное СЛП металлов относится к сложному физико-химическому процессу, в котором плавление, процессы переноса и кристаллизация протекают в малом локальном объеме за короткий период времени. В таких условиях прямое экспериментальное изучение протекающих процессов практически невозможно, так как удается измерить только температуру и форму ванны расплава. Дополнительно после лазерного плавления может быть получена информация о микроструктуре и распределении пор в компакте.

Таким образом, формирование цельного теоретического описания процессов СЛП/ВЛП с помощью ИЛ может быть получено только за счет комбинирования экспериментальных исследований и вычислительного эксперимента [3–6]. В настоящей работе развит двухуровневый подход [7] к моделированию процессов переноса при импульсном селективном лазерном плавлении порошков. Предложен метод разбиения задач на макроскопический и мезоскопический уровни, выполнена алгоритмическая компоновка двухуровневой модели. С использованием двухуровневого подхода описан процесс СЛП порошка карбонильного железа, проведена верификация расчетной модели на доступных экспериментальных данных.

Двухуровневый подход к моделированию СЛП процессов

Метод двухуровневого моделирования основан на известном в литературе подходе расщепления сложной задачи на задачи различных уровней, решения которых согласуются по специально установленной процедуре. Расщепление исходной задачи, как правило, осуществляется на основе анализа пространственно-временных масштабов процессов и их характеристических безразмерных чисел. Такой подход перспективен для анализа процессов СЛП, поскольку изучаемая система обладает несколькими структурными уровнями: всего изделия, слоя порошка, одиночных частиц и элементов первичной кристаллической структуры. По этой причине реализация двухуровневой модели позволяет улучшить прогностическую точность моделей СЛП.

Математически двухуровневый подход основывается на методе редукции числа степеней свободы при сохранении числа уравнений и, соответственно, числа зависимых переменных. Для этого уравнения баланса разбиваются на группы МАКРО и МЕЗО и далее решаются на различных масштабах с выполнением процедуры согласования, рисунок 1. Для этого на основе оценки характеристических чисел процессов переноса, характеристических пространственных масштабов и времен осуществляется декомпозиция полной модели на задачи для макро- и мезоуровней. Каждая задача описывает только одно физическое явление (например, диффузию компонентов, теплоперенос и т.д.), используя в качестве исходных данных поля зависимых переменных, рассчитанные в других задачах, но при этом сохраняется связность модели. Другими словами, в каждое отдельное уравнение входят скалярные или векторные поля, рассчитываемые другими уравнениями. Уточнение краевых условий {Г_i} для мезоскопических моделей, т.е. согласование «сверху-вниз», проводится на основе решения макроскопических моделей. Согласование задач «снизу-вверх» проводится по уточнению зависимостей {F_i} и {G_i} на основе данных мезоскопических моделей.

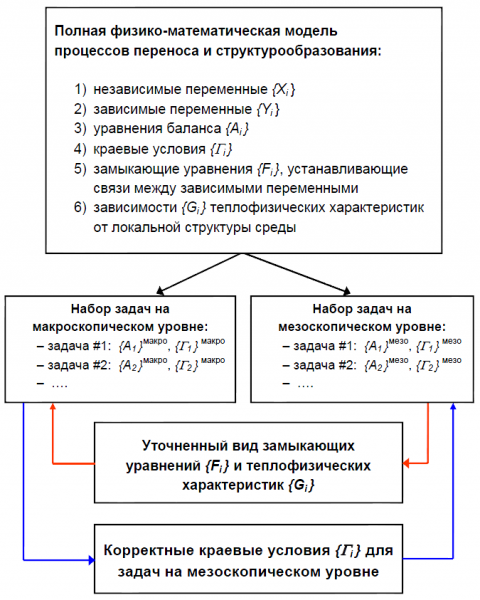
Рисунок 1. Метод разбиения полной модели на задачи макроскопического и мезоскопического уровней

Алгоритмическая компоновка модели

Схема алгоритмической компоновки двухуровневой модели СЛП приведена на рисунке 2. На макроуровне решаются сопряжённые уравнения баланса для температуры T, энтальпии H, пористости e и положения Z границы порошкового слоя соответственно. На мезоуровне осуществляется описание физических эффектов, которые имеют локальный характер. Это анализ эффективной теплопроводности, консолидации порошка и сегрегации химических компонентов. Поскольку все процессы мезоуровня обладают малой корреляционной длиной, задачи мезоуровня допустимо решать как локальные и несопряжённые.

На схеме на рисунке 2 также приведены данные макроуровня, передаваемые с макроуровня на мезоуровень и используемые для постановки краевых задач мезоуровня. К ним относятся поля переменных макроуровня: нестационарное температурное поле T(t, r) и мгновенное распределение e(r) пористости. C мезоскопического уровня на макроуровень передаются замыкающие уравнения, кинетические и термодинамические параметры для уточнения уравнений макроуровня. К ним относятся функция эффективной теплопроводности k_эфф.(e), параметр A кинетической модели усадки и степень сегрегации c_max – c_min компонентов для определения производной dT/dH в уравнении для энтальпии H. Поскольку задачи мезоуровня решаются только в отобранном множестве мезообъёмов, характеризующем все мезообъёмы, то требуется процедура аппроксимации решений в других мезообъёмах. На основании переданных с мезоуровня данных конструируется карта микроструктурных состояний, которая далее интерполируется на всю расчётную область макроуровня. Подробное описание разработанных математических моделей и численных алгоритмов дано в [6, 7].

Рисунок 2. Схема согласования решений на макроскопическом и мезоскопическом уровнях в задаче расчета селективного лазерного плавления

Результаты моделирования на макроуровне

Рассмотрим основные результаты анализа тепловых полей и кинетики усадки в порошковом слое. На рисунке 3 приведены результаты расчёта температуры и формы зоны оплавления при лазерной обработке порошка железа. В области воздействия лазерного луча происходит плавление порошка и консолидация частиц. При этом за счет гауссова распределения энергии в луче происходит плавная усадка по краям, и профиль поперечного сечения имеет чашеобразную форму. Из анализа характерных пространственно-временных масштабов следует, что во время импульса осуществляется интенсивный разогрев поверхностного слоя. Действительно, тепловой поток в подложку на 0,5–1 порядка величины меньше, чем тепловой поток со стороны поверхности, из-за высокой плотности мощности импульсного ЛИ. Охлаждение вследствие радиационного теплопереноса в начале импульса на 2 порядка меньше теплового потока ЛИ и достигает значимых значений от 1 до 5% только при температурах T ~ 2000 К. Конвективное охлаждение в атмосферу на начальных этапах незначительно при T <= T_m, где T_m – температура плавления. В процессе нагрева выше T_mи достижения температур T_кип.кипения (интенсивного испарения) происходит выравнивание потоков подвода тепла и охлаждения. Таким образом, температура поверхности согласно выполненным расчётам никогда не превышала T_кип. После окончания импульса происходит достаточно быстрое остывание за счёт высокой теплопроводности металла, хорошего теплового контакта с подложкой и малого объёма зоны оплавления.

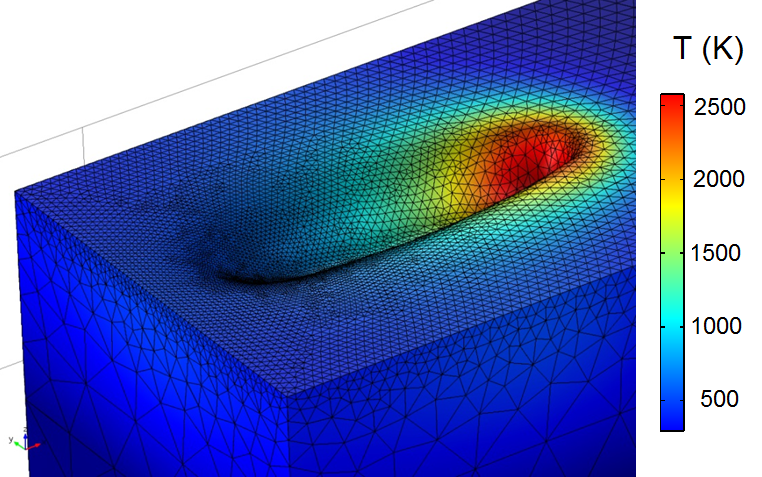
Рисунок 3. Результаты расчёта поля температуры и формы поверхности для слоя порошка железа при прямолинейном движении лазерного луча.

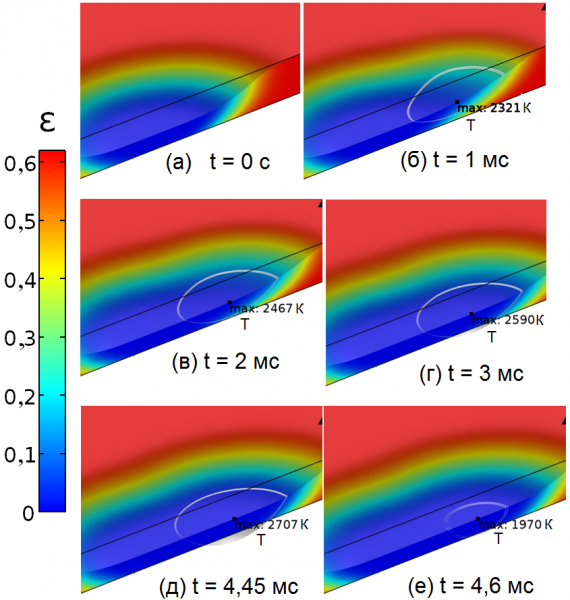
Результаты на рисунке 4 раскрывают кинетику усадки при импульсной обработке. Начальная пористость порошка составляет e₀ = 0,62. Перед началом импульса, рисунок 4(а), имеется сформированная предыдущими импульсами дорожка, в которой вдоль траектории движения луча произошла полная усадка до e = 0. После начала импульса происходит быстрый нагрев выше Tm и формирование зоны оплавления, рисунок 4(б). Как обсуждалось выше, максимальная температура ограничена T < T_кип., но интенсивное испарение стабилизирует температуру в диапазоне 2300 <= T <= 2700 K при T_кип. = 3050 К, рисунок 4(б)–(д). Отметим, что площадь зоны оплавления в течение импульса меняется незначительно. Вместе с тем происходит движение фронта плавления в подложку. На рисунок 4(г) и (д) заметно, что фронт плавления продвинулся дальше границы порошкового слоя и затронул подложку: область оплавления подложки показана серым цветом в нижней части зоны оплавления. Этот механизм оплавления подложки исключительно важен с технологической точки зрения, поскольку обеспечивает формирование трехмерного изделия послойным способом. Площадь зоны оплавления подложки значительно меньше зоны оплавления на поверхности. По этой причине применяется схема сканирования с перекрытием до 80%, что позволяет гарантировать равномерность оплавления подложки. В титановых изделиях ответственного назначения достигается глубина зоны оплавление до h_оплав. = 6 h₀, где h₀ – толщина порошкового слоя. После окончания импульса, рисунок 4(е), зона оплавления быстро затвердевает. Это приводит к возникновению значительных температурных градиентов внутри сплавляемого слоя. Оценки, следующие из расчетных термограмм, рисунок 5, показывают, что температурный градиента в зоне облучения лазерным лучом достигает значений до 105–106 К/м.

14.00

Normal
0

false
false
false

RU
X-NONE
X-NONE

Рисунок 4. Результаты расчeта кинетики плавления и усадки высокодисперсного порошка железа во время импульсного лазерного воздействия. Длительность импульса t = 4,5 мс, мощность лазера P_ИЛ = 50 Вт, частота импульсов n = 100 Гц, радиус луча R_луча = 400 мкм. Цветовой шкалой показано распределение локальной пористости e. Насыпная (начальная) пористость – e₀ = 0,62. Белой линией обозначены изменяющиеся границы зоны оплавления, соответствующие изотерме T = T_m. Время t = 0 с соответствует началу второго импульса

14.00

Normal
0

false
false
false

RU
X-NONE
X-NONE

Рисунок 5. Расчетные термограммы T (t) как функции расстояния контрольной точки до поверхности порошкового слой

Результаты моделирования на мезоуровне

Эффективная теплопроводность порошков зависит от площади теплового контакта частиц, что в конечном итоге определяет термическое сопротивление порошковых сред. Таким образом, важно понимать, как меняется структура порошкового слоя в процессе лазерного нагрева. Было выполнено [8] моделирование консолидации частиц порошка железа методом фазового поля. Гранулометрический анализ показал, что средний размер частиц равен <d> = 3 мкм при очень малой дисперсии s < 1,0 мкм, что связано с технологией его производства термохимическим способом. Таким образом, расчeты для одномодального – с одним размером частиц – порошка могли быть сопоставлены напрямую с результатами лабораторного эксперимента.

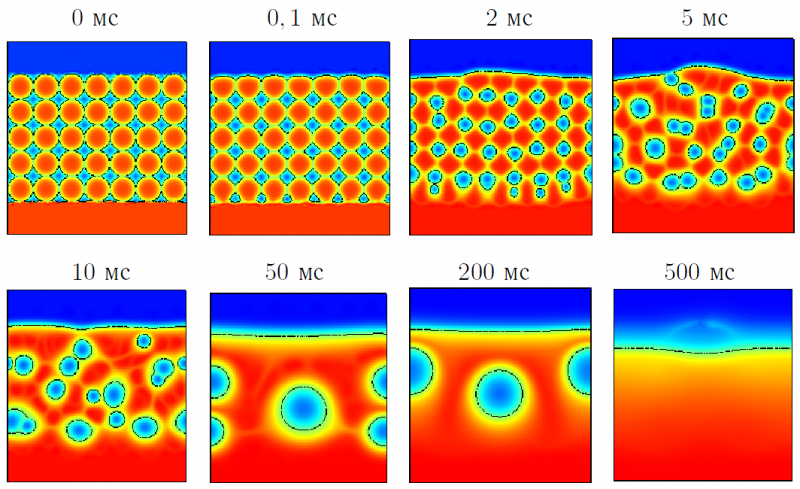
В проведенной серии расчётов исследовалась кинетика консолидации для регулярного массива частиц, рисунок 6. В этом случае каждая частица взаимодействует с несколькими ближайшими соседями в объёме порошкового слоя. На внешней поверхности порошкового слоя число соседей меньше, поэтому происходит быстрое формирование слоя расплава на границе с атмосферой. Анализ изменения структуры фазовых границ на рисунке 6 показывает, что выделяются три стадии консолидации. На первой стадии происходит образование шеек и формирование связного металлического каркаса. На второй стадии реализуется слияние газовых включений и уменьшение удельной поверхности под действием капиллярных сил. На третьей стадии происходит выход газовых включений на поверхность под действием архимедовой силы. Последняя стадия занимает продолжительное время от 50 до 500 мкc, что было объяснено сочетанием двух эффектов: (1) малым объёмом газовых включений и их слабой подъёмной силой, (2) значительным гидродинамическим сопротивлением для сферических включений такого объёма. Этот вывод согласуется с оценкой отношения подъёмной силы и сил вязкого трения, поскольку число Архимеда составляет Ar ~ 10^–6.

14.00

Normal
0

false
false
false

RU
X-NONE
X-NONE

Рисунок 6. Моделирование консолидации расплавленных частиц железа с размером <d> = 3 мкм методом фазового поля

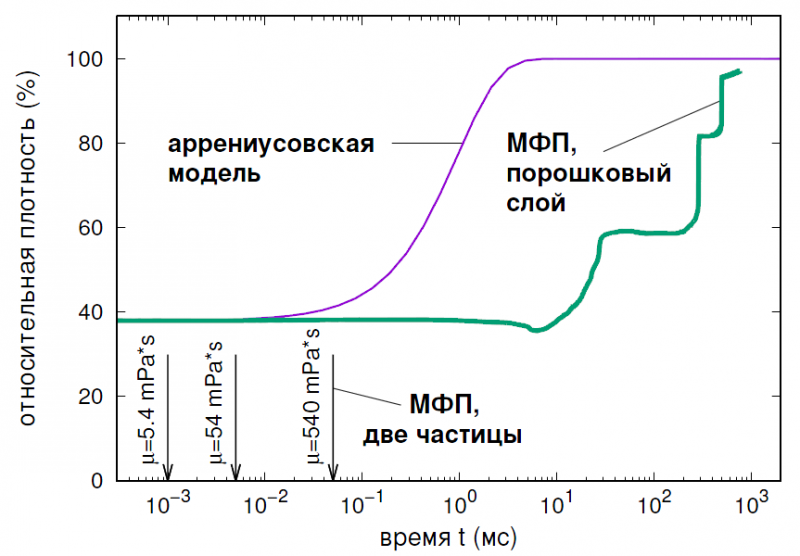
Дальнейший анализ был направлен на изучение кинетики консолидации. На рисунке 7 приведено сравнение результатов фазополевого (ФП) моделирования с кинетической моделью аррениусовского типа, используемой на макроуровне. На графике нанесены данные моделирования как для двух частиц, так и для представительного массива частиц. Кинетическая модель прогнозирует плавное увеличение относительной плотности порошка в интервале времени 0,1 < t <10 мс после начала консолидации. Результаты ФП моделирования показывают двухступенчатую кинетику. Образование шеек заканчивается после 2 мс, и начинается увеличение плотности с 38% до 60% за счёт объединения и выхода на поверхность газовых включений, расположенных близко к внешней поверхности расплава. Отметим, что газовые включения на этой стадии объединены микроканалами, способствующими отводу газа. Как только первая стадия закончена, плотность перестаёт увеличиваться, газовые включения находятся в расплаве, и наблюдается их слияние. Как только достигается достаточный размер для подъёма на поверхность за счёт архимедовой силы, включения выходят на поверхность, и жидкофазная консолидация порошка заканчивается.

14.00

Normal
0

false
false
false

RU
X-NONE
X-NONE

Рисунок 7. Кинетика консолидации порошка железа на диаграмме относительной плотности как функции времени. Толстая линия показывает результаты фазополевого моделирования (МФП). Тонкая линия соответствует полуэмпирической модели
аррениусовского типа. Стрелками указаны характеристические времена консолидации для двух частиц, где m – абсолютная вязкость

Таким образом, на основании данных вычислительного эксперимента можно заключить, что кинетика консолидации является многоступенчатым процессом, и это обусловлено затруднённым выходом газовых включений на поверхность. Данный вывод был нами подтвержден [6] в лабораторном эксперименте для высокодисперсного порошка железа. Таким образом, при импульсной обработке малая длительность импульса способствует формированию структуры с высокой пористостью, что востребовано при производстве каталитически активных функциональных материалов.

Заключение

Основные особенности лазерного плавления металлических порошков были изучены на основе вычислительного эксперимента с использованием развитой в работе двухуровневой модели СЛП / ВЛП процессов. Выполнена серия расчетов для порошка железа, которая показала хорошее соответствие расчетных результатов данным лабораторного эксперимента. Получено хорошее согласие для плотности поровых дефектов и удовлетворительное согласие для формы одиночной дорожки после кристаллизации.

Установлено, что консолидация частиц порошка и усадка порошкового слоя происходят по двухэтапной схеме, когда на первом этапе реализуется формирование связного пористого каркаса и консолидация газовых включения, на втором этапе происходит вывод газовых включений на поверхность. Прогнозирование второго этапа исключительно важно для контроля остаточной пористости в СЛП / ВЛП процессах.

Показано, что подбор параметров лазерного излучения для ИЛ позволяет варьировать в широком диапазоне режимы кристаллизации ванны расплава и, соответственно, формируемые механические и физико-химические свойства компактов. Достижимы режимы сплавления с малым временем кристаллизации, когда ванна расплава полностью затвердевает между импульсами. В итоге это позволяет обеспечить высокие температуры и высокие скорости кристаллизации в зоне лазерного облучения, что необходимо для формирования высоконеравновесных фазовых состояний и микроструктур.

Работа выполнена при финансовой поддержке РФФИ, проект р_мол_а № 18-47-183002.

Авторы: Кривилев М.Д., Гордеев Г.А., Анкудинов В.Е., Харанжевский Е.В.

Удмуртский государственный университет,

Россия, Удмуртия, г. Ижевск, ул. Университетская, 1, 426034

E-mail: mk@udsu.ru

Список литературы

1. Шишковский И.В. Основы аддитивных технологий высокого разрешения / СПб.: Питер. 2016. – 400 c..

2. Харанжевский Е.В. Высокоскоростное лазерное спекание металлических высокодисперсных порошков и композиционных материалов с металлической матрицей / дисс. д-ра техн. наук, Ижевск, УдГУ. 2016. – 379 с.

3. King W.E., Anderson A.T., Ferencz R.M., Hodge N.E., Kamath C., Khairallah S.A., Rubenchik A.M. Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges / Applied Physics Reviews. 2015. – Vol. 2, No. 4. – P. 041304.

4. Knyazeva A., Kryukova O. Coating combustion synthesis controlled by moving electron beam / IOP Conf. Series: Journal of Physics: Conf. Series. 2018. – Vol. 1115, P. 042028.

5. Кривилев М.Д., Харанжевский Е.В., Гордеев Г.А., Анкудинов В.Е., Управление лазерным спеканием металлических порошковых смесей / Управление большими системами. 2010. – № 31, C. 299-322.

6. Гордеев Г.А., Кривилев М.Д., Анкудинов В.Е. Компьютерное моделирование селективного лазерного плавления высокодисперсных металлических порошков / Вычислительная механика сплошных сред. 2017. – Т. 10, № 3. – С. 293-312.

7. Кривилев М.Д. Двухуровневое математическое моделирование процессов переноса и структурообразования в металлургии мезоскопических объемов / дисс. д-ра физ.-мат. наук, Ижевск, УдГУ. 2018. – 316 с.

8. Krivilyov M.D., Mesarovic S.Dj., Sekulic D.P. Phase-field model of interface migration and powder consolidation in additive manufacturing of metals / J. Mater. Sci. 2017. – Vol. 52, Iss. 8. – P. 4155-4163.