Введение
В ТГПУ им. Л.Н. Толстого выполняется прикладная научно-исследовательская работа по теме «Разработка прототипа инженерного программного обеспечения (ИПО) на основе высокопроизводительных вычислений для оценки механических характеристик изделия, изготовленного с использованием аддитивных технологий (методом селективного лазерного спекания) с учетом стратегии изготовления изделия», в рамках которой исследуются возможности и технологии применения параллельных вычислений. Показано, что учет особенностей моделирования процессов селективного лазерного спекания может быть осуществлён с применением сетей Петри-Маркова, в которых сочетаются аспекты, релевантные случайным процессам в модулях параллельной вычислительной системы, и аспекты, описывающие логику их взаимодействия. Актуальность темы определяется тем фактором, что в условиях перехода к цифровой экономике процессы анализа прочностных характеристик материалов можно осуществлять на основе компьютерного моделирования.
Основная часть
Особую роль в последнее время играют материалы, получаемые при использовании аддитивных технологий. В свою очередь, это порождает проблему разработки математического, алгоритмического и программного аппарата моделирования характеристик изделий, изготовленных из таких материалов. Указанная проблема во всех индустриально развитых странах мира решается путем замены реального объекта его математической моделью, воспроизводящей основные функции оригинала и подобной ему в заданных релевантных аспектах. Одним из ключевых препятствий, сдерживающих массовое внедрение аддитивных технологий в машиностроительное производство, является отсутствие однозначного прогнозирования прочностных характеристик изготавливаемых металлических деталей на этапе их проектирования, что ограничивает сферу промышленного применения аддитивных технологий по сути лишь изготовлением макетов.
Предпосылки научной проблемы заключаются в том, что свойства материала изделия, изготовленного с помощью метода селективного лазерного спекания, могут существенно отличаться от исходных свойств этого материала. В наибольшей степени это относится к изделиям из металлов. При их изготовлении с помощью аддитивных технологий в качестве сырья используется металлический порошок, частицы которого спекаются в процессе изготовления.
Кроме того, при изготовлении таких изделий их части подвергаются локальным воздействиям высоких температур, что приводит к значительным температурным деформациям. В результате материал изделия может оказаться пористым, т.е. структурно-неоднородным, и при этом в нем возникают остаточные микронапряжения, которые могут быть конечными (не малыми). Как следствие, большие локальные температурные деформации могут привести к потере устойчивости изделия в процессе его изготовления. Поэтому прочностные свойства изделий, изготовленных с помощью метода селективного лазерного спекания, существенно зависят от особенностей технологии их изготовления. Оценка прочностных свойств таких изделий, в особенности металлических изделий, представляет собой нетривиальную научную задачу. При том, что существующие модели не в полной мере учитывают явления и процессы, происходящие в гетерогенных структурах изделий, и нуждаются в уточнении и совершенствовании.
В настоящее время не существует отечественных программных продуктов, позволяющих моделировать тепловое и напряженно-деформированное состояние изделия в процессе его создания методом селективного лазерного спекания с учетом стратегии изготовления изделия. Указанные обстоятельства определяют актуальность выполнения ПНИЭР.
Целью и научно-технической проблемой проекта является разработка научно-технических решений в области создания программного обеспечения для предсказательного многомасштабного физического моделирования теплового и напряженно-деформированного состояния изделия в процессе его создания методом селективного лазерного спекания с учетом стратегии изготовления изделия с использованием метода конечных элементов, метода спектральных элементов.
Таким образом, исходя из сложившейся ситуации на рынке ИПО, характеризующейся преобладанием импортных программных продуктов, разработка отечественного инженерного программного обеспечения является весьма актуальной задачей, в том числе, инженерного программного обеспечения для анализа прочности изделий, получаемых с использованием аддитивных технологий.
Основной задачей программного обеспечения является расчёт прочностных характеристик изготавливаемых металлических деталей на этапе их проектирования. В основе расчёта лежат современные математические методы расчета, использующие параллельные вычисления для существенного увеличения скорости и точности расчета, что будет являться уникальным конкурентным преимуществом по сравнению с конкурентными аналогами. Инструментом распараллеливания решения задач методом конечных элементов является технология MPI. В случае технологии MPI необходимо разрабатывать алгоритм распараллеливания вычислительных процессов для программирования метода конечных элементов таким образом, чтобы представить решение задачи в виде совместного действия нескольких независимых процессов с независимыми данными.
Необходимость оптимального разбиения алгоритма на параллельно выполняемые фрагменты делает актуальной задачу оценки вычислительной сложности фрагментов алгоритмов, реализуемых в компонентах вычислительных систем, а также вычислительной сложности алгоритма, реализуемого в параллельной вычислительной системе, в целом.
В настоящее время параллелизм является доминирующей парадигмой в организации вычислительного процесса. Если в области проектирования специализированных ЭВМ идеи параллелизма используются на практике более пятидесяти лет (CDC-6600 1964 года [1] включает десять независимых функциональных устройств, работающих одновременно), то в современных условиях параллельные вычисления практикуются, кроме собственно многопроцессорных ЭВМ, в многоядерных процессорах и сетях ЭВМ [2]. При организации вычислительного процесса в подобных структурах разработчики сталкиваются с проблемой неоптимального использования аппаратных средств параллельных структур, что связано с низким коэффициентом загрузки процессоров, конфликтами при доступе к совместно используемым ресурсам и т.п. [3]. Решение проблемы разрешения конфликтов и повышения коэффициента загрузки приводит к необходимости такой организации программной обработки данных, которая сокращала бы вычислительную сложность до некоторого минимального уровня. Интуитивно можно предположить, что время решения задачи в параллельной вычислительной системе может изменяться от величины, получающейся в случае, когда все операторы алгоритма последовательно интерпретируются одним процессором (верхний предел), до величины, получающейся, когда все компоненты начинают и заканчивают интерпретацию своих частей алгоритма одновременно, и при решении задачи исключены случаи их простоя (нижний предел). Необходимость оптимального разбиения алгоритма на параллельно выполняемые фрагменты делает актуальной задачу оценки вычислительной сложности фрагментов алгоритмов, реализуемых в компонентах вычислительных систем, а также вычислительной сложности алгоритма, реализуемого в параллельной вычислительной системе, в целом.
В [1] на основе исследования процесса выполнения команды процессором фон-Неймановской ЭВМ было показано, что для внешнего наблюдателя количество машинных тактов, затрачиваемое процессором на ее выполнение, является случайной величиной, распределение которой зависит как от особенностей аппаратных средств, так и от распределения обрабатываемых командой данных. Кроме того, в [2] был исследован характер переходов между операторами алгоритма для внешнего наблюдателя и показана его квазистохастичность. Поэтому при оценке временной сложности требуется привлечение теории случайных, в частности Марковских (а в более общем случае, полумаровских) процессов, крупный вклад в развитие которых внесли Ю.К. Беляев, Б.В. Гнеденко, Д.Р. Кокс, Д. Ллойд, В.Л. Смит, В. Харрис, А.М. Широков. Результаты их научных трудов легли в основу математического аппарата оценки временной сложности алгоритмов, однако особенности параллельной обработки выдвигают задачу дальнейшего развития существующей теории.
Методология моделирования собственно параллельных процессов заложена в трудах К. Петри, В. Рейзига, Дж. Питерсона, В.Е. Котова [4-8], где для исследования параллелизма применен аппарат сетей Петри. Ситуационный (причинно-следственный) характер связей между позициями и переходами сетей Петри [4] является предпосылкой для моделирования, во-первых, структур алгоритмов, а во-вторых - логики событий, происходящих в параллельных системах. Однако, являясь асинхронными по определению, модели указанного типа позволяют лишь ответить на вопросы о принципиальной достижимости состояний системы, соответствующих заданным требованиям, но спрогнозировать моменты наступления тех или иных состояний в физическом времени с помощью сетей Петри, в их классической интерпретации, невозможно.
Помимо РСП широкое распространение получило другое расширение классической теории сетей Петри – временные сети Петри. В указанную модель введены счетчики для контроля локального или глобального времени. В ней также определены временные характеристики пребывания фишек в позициях, генерации/умирания фишек по истечении заданного времени и т.п. Наиболее популярными стали модели, в которых временные характеристики связаны с переходами, а именно дискретно-временная модель Рамхандани-Штарке и непрерывно-временная модель Мерлина. Попытки приспособить сети Петри для определения временных интервалов (time-extended Petri nets) предпринимались и рядом других авторов [9]. Однако даже в модифицированном варианте временные сети Петри не позволяют учитывать все многообразие взаимодействий в системах, что связано, в частности с ограниченностью логических условий продолжения процессов элементарной конъюнкцией.
В целом методология формирования моделей, ориентированных на оценку вычислительной сложности алгоритмов, реализуемых в параллельных вычислительных системах, должна учитывать следующие их особенности: определенную и специфичную для каждой параллельной системы стратегию использования ресурсов для обработки информации; динамический характер высвобождения/задействования вычислительных ресурсов в процессе решения конкретных задач; необходимость обмена данными (промежуточными результатами) между вычислительными модулями и связанная с этим явлением необходимостью синхронизации функционирования процессоров; наличие эффекта "соревнования" между параллельно функционирующими компонентами.
Наиболее полно учет названных особенностей может быть осуществлен в моделях, называемых сетями Петри-Маркова (СПМ), в которых сочетаются аспекты, релевантные случайным процессам в модулях параллельной вычислительной системы, и аспекты, описывающие логику их взаимодействия. В моделях исследуемого типа на структуры, учитывающие параллелизм, накладываются стохастико-временные параметры полумарковских процессов в отдельных вычислительных модулях и логические условия взаимодействия.
Самый общий подход к заданию СПМ основан на построении системы множеств, их описывающих. Сетью Петри-Маркова называется структурно-параметрическая модель, заданная множеством:
![]() , (1)
, (1)
где ![]() – множество, описывающее структуру двудольного ориентированного графа, представляющего собой сеть Петри; A = {a1(a), ..., aj(a), ..., aJ(a)} – конечное множество позиций; Z = {z1(z), ..., zj(z), ..., zJ(z)} – конечное множество переходов; J(a) - мощность множества позиций; J(z) – мощность множества переходов;
– множество, описывающее структуру двудольного ориентированного графа, представляющего собой сеть Петри; A = {a1(a), ..., aj(a), ..., aJ(a)} – конечное множество позиций; Z = {z1(z), ..., zj(z), ..., zJ(z)} – конечное множество переходов; J(a) - мощность множества позиций; J(z) – мощность множества переходов; ![]() – матрица смежности размером J(a) х J(z), отображающая множество позиций в множество переходов;
– матрица смежности размером J(a) х J(z), отображающая множество позиций в множество переходов; ![]() – матрица смежности размером J(z) х J(a), отображающая множество переходов в множество позиций;
– матрица смежности размером J(z) х J(a), отображающая множество переходов в множество позиций; ![]() – параметры, накладываемые на структуру П, и определяющие временные, вероятностные и логические характеристики СПМ; q = (q1(z), ..., qj(z), ..., qJ(z)) – вектор, определяющий вероятность начала процесса в одном из переходов множества Z; h(t) – [hj(a)j(z)(t)] – полумарковская матрица размером J(a) х J(z); t – время;
– параметры, накладываемые на структуру П, и определяющие временные, вероятностные и логические характеристики СПМ; q = (q1(z), ..., qj(z), ..., qJ(z)) – вектор, определяющий вероятность начала процесса в одном из переходов множества Z; h(t) – [hj(a)j(z)(t)] – полумарковская матрица размером J(a) х J(z); t – время; ![]() – матрица логических условий размером J(a) х J(z); IA(Z) = {IA(z1(z)), ..., IA(zj(z)), ..., IA(zJ(z))} и OA(Z) = {ОA(z1(z)), ..., ОA(zj(z)), ..., ОA(zJ(z))} – соответственно входная и выходная функции переходов;
– матрица логических условий размером J(a) х J(z); IA(Z) = {IA(z1(z)), ..., IA(zj(z)), ..., IA(zJ(z))} и OA(Z) = {ОA(z1(z)), ..., ОA(zj(z)), ..., ОA(zJ(z))} – соответственно входная и выходная функции переходов;
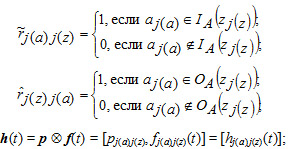 (2)
(2)
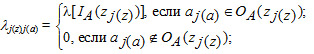 (3)
(3)
p = [pj(a)j(z)] – матрица вероятностей переключений полумарковского процесса из позиции aj(a) в смежный переход zj(z); f(t) = [fj(a)j(z)(t)] – матрица плотностей распределения времени пребывания полумарковского процесса в позиции aj(a) с последующим переключением в переход zj(z); ![]() - знак прямого произведения матриц.
- знак прямого произведения матриц.
На вероятности и плотности распределения накладываются ограничения:
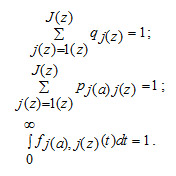
При численном анализе процессов параллельных вычислительных системах могут быть заданы: p = (pj(a)j(z)) – матрица вероятностей; T = (Tj(a)j(z)) – матрица математических ожиданий, определяемая в виде
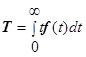 , (4)
, (4)
D = (Dj(a)j(z)) – матрица дисперсий, определяемая в виде
 . (5)
. (5)
Таким образом, разработан эффективный и достаточно несложный математический аппарат для моделирования параллельных вычислительных систем, ориентированный на оценку временной сложности алгоритмов, реализуемых в них. В моделях наряду со структурными и временными аспектами их функционирования отражается логика взаимодействия компонентов параллельных вычислительных систем.
Работа выполнена в рамках Федеральной программы «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2014-2020 годы» в ТГПУ им. Л.Н. (проект №14.577.21.0271, уникальный идентификатор проекта RFMEFI57717X0271).
Авторы:
Привалов А.Н. a, Богатырева Ю.И.
Тульский государственный педагогический университет им. Л.Н. Толстого,
Россия, г.Тула, пр. Ленина, 125, 300026
aE-mail: iprivalov.61@mail.ru
Список литературы
1. Bell G.C. Multis: A new class of multiprocessor computers // Science. – 1985. – Vol. 228, Iss. 4698. – P. 462–467.
2. Culler D., Singh J., Gupta A. Parallel computer architecture: a hardware/software approach / San Francisco: Morgan Kaufmann Publishers Inc., 1999.
3. Lewis T.G. Foundations of Parallel Programming: a Machine-Independent Approach / Los Alamitos, CA : IEEE Computer Society Press. – 1997.
4. Petri C.A. Nets, time and space // Theoretical Computer Science. – 1996. – Vol. 153, Iss. 1-2. – P. 3–48.
5. Reisig W. Elements Of Distributed Algorithms: Modeling and Analysis with Petri Nets / Berlin, Heidelberg : Springer-Verlag, 1998.
6. Reisig W. Correctness proofs of distributed algorithms // Selected Papers of International Workshop “Theory and Practice in Distributed Systems”. – Germany. Dagstuhl Castle, 1994. – P. 164–177.
7. Peterson J.L. Petri Net Theory and the Modeling of Systems / Prentice Hall. – 1981.
8. Котов В.Е. Сети Петри / М.: Наука. – 1984.
9. Привалов А.Н. Моделирование информационных процессов в вычислительной подсистеме тренажерных систем специального назначения / Тула : Тульский государственный университет. – 2009, 215 с.



