14.00

Normal
0

false
false
false

RU
X-NONE
X-NONE

  Введение  

Разработан программный комплекс, позволяющий проводить расчёты для произвольно нагруженной плоскости с непересекающимися прямолинейными трещинами, а также плоскости с цепочкой прямолинейных трещин при малом расстоянии между кончиками. Отношение расстояния между кончиками трещин к длине самой короткой трещины может достигать при расчётах 10-45.

Программный комплекс позволяет вычислять: напряжения на берегах трещин, значения коэффициентов интенсивности напряжений (КИН), поля напряжений, распределение скачка перемещений вдоль линий трещин и значения коэффициентов тензора модулей податливости.

Составление системы линейных уравнений

Расчёты проводятся следующим образом: вдоль линий трещин распределяются узловые точки и составляется система линейных уравнений на основании коэффициентов взаимного влияния узловых точек друг на друга. Коэффициенты вычисляются на основании формул для напряжений вызванных парой точечных сил, приложенных к берегам трещины [2].

Для системы из N произвольно ориентированных линейных трещин вдоль линий трещин распределяется некоторое количество узловых точек. Ориентация трещин задаётся единичными векторами нормалей к трещинам – n_i(i = 1 ÷ N). Известны формулы для вычисления в любой точке плоскости компонентов {_xx, _xy, _yy} тензора напряжений, вызванных парой точечных нормальных и сдвиговых сил, приложенных к берегам трещины.

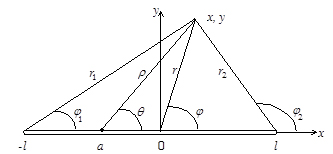
Рисунок 1. Иллюстрация к формулам (2) и (3)

Компоненты тензоров напряжений ⁿ и ^t (1) в точке с координатами (x, y) (см. рисунок 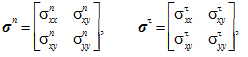1)

(1)

вызванных в точке a парой точечных сил t ⁿ(a) действующих нормально к линии трещины и парой точечных сдвиговых сил t(a) действующих вдоль линии трещины вычисляются по формулам (2) и (3) из [2] (принятые обозначения проиллюстрированы на рисунке 1):

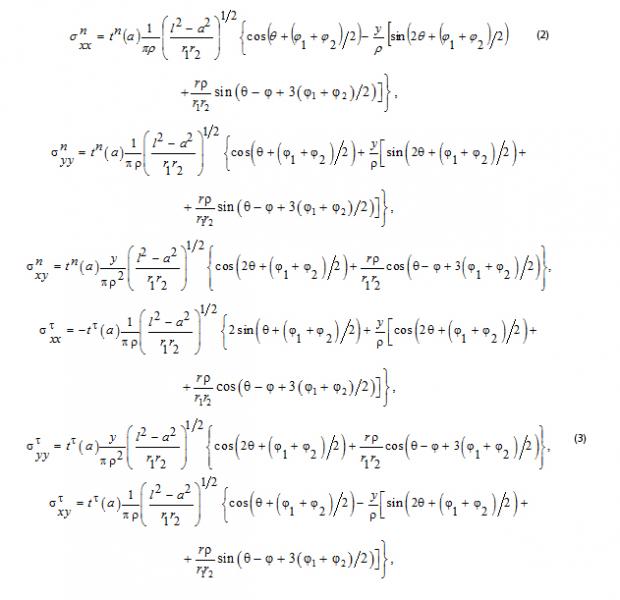
Для произвольной точки линейной трещины, на основании формул (2) и (3), можно вычислить коэффициенты её влияния () на любую точку другой линейной трещины, как

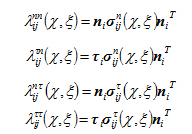
где  – удельные коэффициенты влияния точки j-й трещины на точку i-й трещины, численно равные нормальному и сдвиговому напряжениям вызванным в точке i-й трещины, точечными единичными нормальными силами, приложенными к x точке j-й трещины;

 – удельные коэффициенты влияния точки j-й трещины на точку i-й трещины, численно равные нормальному и сдвиговому напряжениям вызванным в точке i-й трещины, точечными единичными сдвиговыми силами, приложенными к точке j-й трещины;

n_i – единичный вектор нормали к i-й трещине;

_i – единичный вектор направленный вдоль i-й трещины, полученный поворотом n_i на 90° по часовой стрелке;

– тензор удельных напряжений в точке   i-й трещины, вызванных точечными единичными силами действующими нормально к линии трещины в точке j-й трещины;

– тензор удельных напряжений в точке   i-й трещины, вызванных точечными сдвиговыми силами действующими вдоль линии трещины в точке j-й трещины;

Далее, для выбранных узловых точек составляется система линейных уравнений относительно нормальных и сдвиговых напряжений вида (4), отдельная пара строк которой (составленная для точки i-й трещины) содержит:

– в левой части – разность общего напряжения в узловой точке i-й трещины и напряжений, вызванных в данной точке остальными трещинами,

– в правой части значение напряжения, вызванного в узловой точке i-й трещины внешней нагрузкой

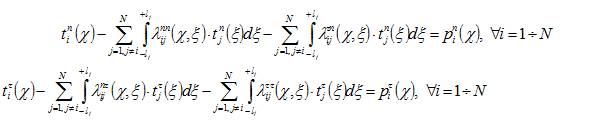(4)

где

l_j – полуширина j-й трещины;

–l_i <= <= +l_i – параметр задающий расстояние от центра i-й трещины до некоторой точки i-й трещины;

–l_j<=  <= +l_j – параметр задающий расстояние от центра j-й трещины до некоторой точки j-й трещины;

tⁿ_i() и t_i() – результирующие напряжения (нормальные и сдвиговые) в точке i-й трещины;

pⁿ_i() и p_i() – нормальное и сдвиговое напряжения вызванных внешней нагрузкой в точке i-й трещины.

Решением данной системы уравнений является вектор полных напряжений в каждой из узловых точек.

Использование метода Ньютона-Котеса

Для вычисления интегралов в левой части (4) был применён метод Ньютона-Котеса [4]. Интеграл от произведения _ij(,) и t_j() интерполировался на каждом отрезке интегрирования (между двух соседних узловых точек q и q+1), по равноотстоящим промежуточным точкам, многочленом Лагранжа, для которого значение интеграла вычисляется аналитически:

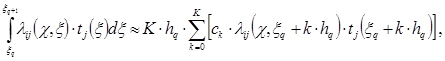(5)

где

 - интервал между соседними промежуточными точками;

K – порядок интерполяционного многочлена;

_q – положение q-й узловой точки j-й трещины относительно центра j-й трещины.

Сами коэффициенты c_k вычислялись по формуле:

Интеграл от произведения  _ij(,) и t_j() вдоль линии j-й трещины от – l_j до + l_j в соответствии с формулой (5) может быть представлен, как:

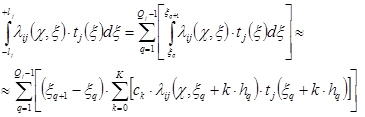
где Q_j– количество узловых точек j-й трещины.

Обозначим множество узловых и промежуточных точек j-й трещины, как v_jr = _q + kh_q , а множество весовых коэффициентов при произведении  _ij(,)×t_j(), как w_jr (просуммировав весовые коэффициенты w_jr для повторяющихся значений r):

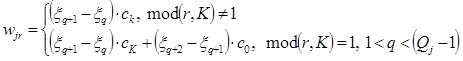
где j = 1 ÷ N, q = 1÷ (Q_j – 1), k = 0 ÷ K, а r = 1 + k + (q – 1)×K и запишем окончательное выражение в виде:

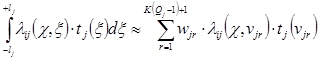
Поскольку для вычисления отдельной строки в (4) необходимо иметь значения нормальных и сдвиговых напряжений в для узловых и промежуточных точек каждой из трещин, то есть tⁿ_j (v_jr ) и t_j (v_jr ) для j = 1 ÷ N и r = 1÷[1 + (Qj – 1)×K], система линейных уравнений (4) будет составляться и решаться относительно этих узловых и промежуточных точек, её отдельная пара строк будет иметь вид:

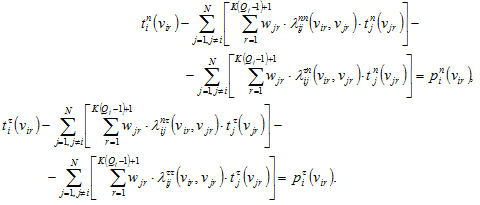
Значения коэффициентов влияния трещины на узловые точки других трещин обратно пропорциональны расстоянию до этих точек. Напряжения также обратно пропорциональны расстоянию до соседних трещин, что приводит к возникновению больших значений напряжений и КИН (см. таблицу 1). Всё это при малых расстояниях между трещинами затрудняет получение точного решения. В связи с этим при составлении системы линейных уравнений применялся метод Ньютона-Котеса 45-го порядка, а вычисления производились с использование пакета Multiprecision Computing Toolbox [1] с разрядностью до 55 десятичных значащих цифр.

Таблица 1. Сравнение прямолинейной трещины с эквивалентной цепочкой коллинеарных трещин (см. рисунок 2) при вертикально приложенной растягивающей нагрузке ( = 1)

Проверка

Для нагруженной плоскости с цепочками из двух коллинеарных трещин равной длины (см. рисунок 2) существуют точные аналитические решения для КИН (K_I), которые приводятся в справочнике [3]. Эти решения использовались для оценки точности программного комплекса. Для двух трещин (см. рисунок 2) при длинах трещин 2a = 1 и расстоянии между кончиками трещин 2k = 10^-45 относительная ошибка программного комплекса, не превышала: K_IA < 0.003% и K_IB < 0.019%.

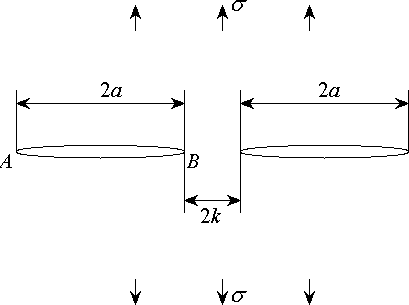
Рисунок 2. Бесконечная равномерно нагруженная плоскость с двумя коллинеарными трещинами

На рисунке 3 сравниваются раскрытие одной трещины (жирная чёрная линия) и цепочки из нескольких трещин имеющей ту же длину (далее, эквивалентной цепочки трещин) при вертикально приложенной растягивающей нагрузке. Из рисунка видно, что при уменьшении расстояния между кончиками трещин 2k, раскрытие цепочки трещин асимптотически приближается к раскрытию одной трещины, а относительная разность среднего раскрытия <b> цепочки трещин и одной трещины приблизительно пропорциональна [lg(2k)]^-1. Аналогичная зависимость наблюдается для коэффициентов интенсивностей напряжений на концах цепочки коллинеарных трещин K_IA и одной прямолинейной трещины (см. Таблицу 1).

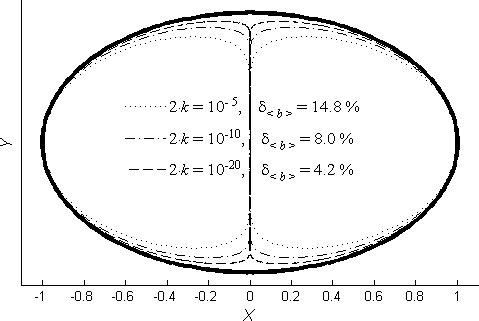
Рисунок 3. Раскрытие цепочек из нескольких коллинеарных трещин при вертикальной растягивающей нагрузке

Выводы

На основании сказанного выше, можно сделать вывод, что одна прямолинейная трещина, при оценке её вклада в эффективные свойства и при вычислении КИН, с некоторой погрешностью может быть заменена эквивалентной цепочкой коллинеарных трещин. Эквивалентная цепочка трещин делает меньший вклад в эффективные свойства и имеет меньшие абсолютные значения КИН на концах цепочки чем прямолинейная трещина, но это отличие уменьшается обратно пропорционально логарифму расстояния между кончиками трещин в цепочке.

Благодарности

Работа выполнена в Федеральном государственном бюджетном образовательном учреждении высшего образования Нижегородский государственный технический университет им. Р.Е. Алексеева (НГТУ), при финансовой поддержке государства в лице министерства образования и науки Российской Федерации в рамках договора №14.Z50.31.0036. Направление научного исследования: «Создание научной лаборатории композиционных и керамических материалов с применением к Арктическим транспортным средствам (LCCM)».

Автор: Мартынюк М.В.

Нижегородский государственный технический университет им. Р.Е. Алексеева, Россия, г. Нижний Новгород, ул. Минина, 24, 603950

E-mail: m_mart@mail.ru

Список литературы

1. ADVANPIX Multiprecision Computing Toolbox for MATLAB : official site. – Yokohama. – URL: https://www.advanpix.com (access date: 14.01.19).

2. Kachanov M.L. Elastic Solids with Many Cracks and Related Problems / Advances in Applied Mechanics – Massachusetts: Academic Press, 1994. – P. 256-426.

3. Murakami Y. Stress Intensity Factors Handbook / In 2 Volumes. Y. Murakami, (Editor in Chief), M.T. Hasebe, Y. Itoh, K. Kishimoto, H. Miyata, N. Miyazaki, H. Terada, K. Tohgo and R. Yuuki,(Co-editor), Oxford etc.: Pergamon press, 1987.

4. Whittaker E. T., Robinson G. The Newton-Cotes Formulae of Integration. § 76 The Calculus of Observations: A Treatise on Numerical Mathematics / 4th ed. New York: Dover, 1967. – P. 152-156.